2023. 12. 1. 11:31ㆍ통계학
빈도분포표(frequency distribution)와 그래픽 기술(graphical techniques)은 데이터 정보를 표현하는데 유용한 도구들이다. 특히 빈도분포표와 그래픽의 장점은 양적정보(quantitative information)를 쉽게 이해할 수 있도록 요약해준다는 것이다.
하지만 때로는 방대한 다변량 데이터(multivariate data)를 분석해야 하는데 이 경우 그래프와 표가 효율적이지 못하다.
예를 들어, 우리가 남성과 여성들의 소득수준, 교육수준, 정치적 성향에 대한 정보를 표현하고자 할때 이러한 정보들을 표나 그래프로 표현하려면 엄청나게 많은 표와 그래프들이 필요하다.
분석하고자 하는 변수들이 늘어날수록 정보들을 분명하게 나타내기가 어려워진다. 결국 연구자들이 아주 혼란스러워 진다.
따라서, 데이터의 분포를 하나의 숫자로 선택해서 보다 더 간결하게 요약해줄 필요가 있다.
이것이 중심경향치(Central tendency)이다.
중심경향치는 평균치 또는 분포를 대표하는 숫자(값)을 의미한다.
최빈값(Mode), 중앙값(Median), 평균(Mean) 들이 중심경향치에 속한다.
- 최빈값(Mode)
최빈값은 가장 빈도가 높은 범주(category)나 값(score)을 말한다.
아래 표 3.1에는 미국에서 자주 사용되는 외국언어들과 사용인구 숫자가 나와있다.
가장 자주 사용되는 언어(최빈값)는 무엇인가?

최빈값(Mode)은 당연히 스페인어이다.
아래 막대그래프는 교육수준별 숫자가 나와있다. 최빈값(Mode)은 무엇인가?

대졸과 전문대졸이 모두 43명으로 같다. 이 경우 대졸과 전문대졸이 모두 최빈값(Mode)이다.
- 중앙값(Median)
중앙값(Median)은 중심경향치 중의 하나로서 서열척도(ordinal scale) 수준의 변수부터 사용이 가능하다.
중앙값(Median)은 데이터 분포에서 정확하게 중앙에 위치하는 값을 말한다. 따라서 분포의 절반은 중앙값 위에 존재하고 절반은 중앙값 아래에 존재한다.
* 홀수로 분류되어 있는 데이터에서 중앙값(Median)을 찾아라!
홀수로 분류되어 있는 데이터 에서 중앙값 찾는 공식은 '(N+1)/2' 이다.

중앙값은 3번째 이므로 좋다(Good)이 정답이다.
* 짝수로 분류되어 있는 데이터에서 중앙값(Median)을 찾아라!
짝수는 홀수보다 약간 더 복잡하다.
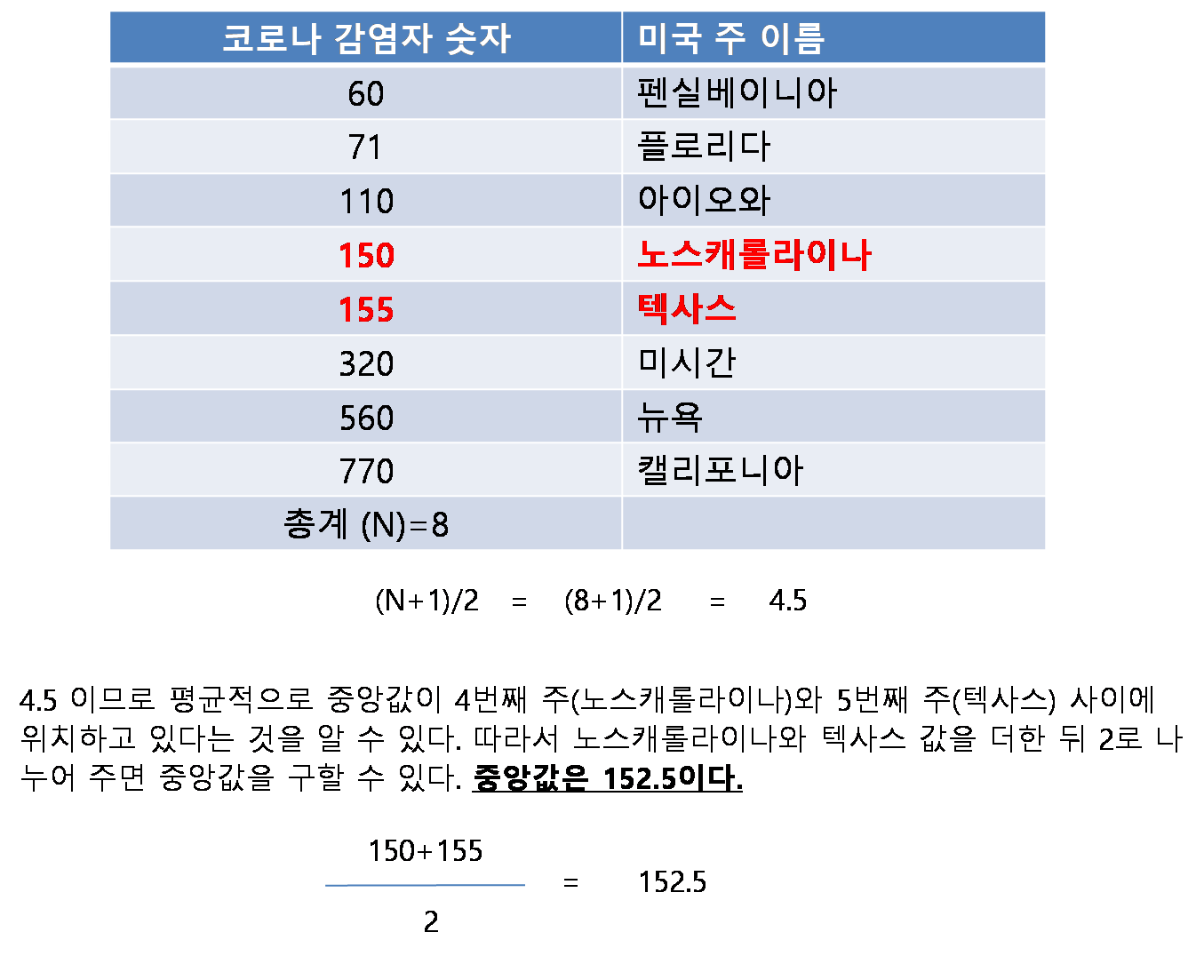
* 빈도분포표(Frequency distribution)에서 중앙값(Median)을 찾아라!

- 평균(Mean)
평균(mean)값은 중심경향치 중 하나로서 주어진 모든 값들을 더한뒤에 값들의 총갯수로 나누어준 값이다. 이것은 산술상의 평균치(arithmetic average)이다.
* 평균구하는 공식

직접 평균을 구해보자!

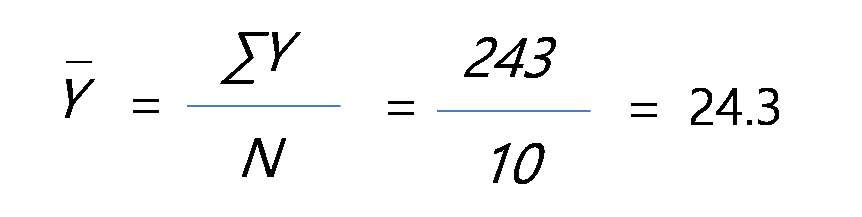
'통계학' 카테고리의 다른 글
| [통계학] 데이터의 정리와 그래픽 제시 (1) | 2023.12.01 |
|---|---|
| 연구과정 (The Research Process) (0) | 2023.11.30 |
| 통계측정방법: 척도(Scale)의 종류 (0) | 2023.11.30 |
| 통계란 무엇인가? (1) | 2023.11.30 |